前言
DFS(Depth First Search,深度度优先搜索):其思路为不撞南墙不回头,从起点开始一层一层向下搜索,如果可以无法继续往下,则一直回溯到可向下搜索的结点,再继续向下搜索,直至全部搜索完成。(建议与BFS共同阅读)
实现思路(建议用简单数据手写模拟运行):
1.将起点标记为已搜索
- 进入dfs(),判断是否结束返回
- 搜索下一未搜索过的结点,标记并dfs(下一结点)
咳咳:DFS用栈(递归),BFS用队列
简单介绍后根据思路尝试一道水题吧
洛谷P1605 迷宫
#include <bits/stdc++.h>
using namespace std;
int N,M,T,SX,SY,FX,FY,ans;
int a[9][9],b[9][9];
int ntx[4]={0,0,-1,1};
int nty[4]={1,-1,0,0};
void dfs(int x,int y){
if(x==FX&&y==FY) {
ans++;
return;
}
int i,nx,ny;
for(i=0;i<4;i++){
nx=x+ntx[i];
ny=y+nty[i];
if(nx>0&&nx<=M&&ny>0&&ny<=N&&b[nx][ny]==0&&a[nx][ny]==0){
b[nx][ny]=1;
dfs(nx,ny);
b[nx][ny]=0;
}
}
}
int main()
{
int i,j,x,y;
cin>>N>>M>>T>>SX>>SY>>FX>>FY;
b[SX][SY]=1;
for(i = 0;i<T;i++){
cin>>x>>y;
a[x][y]=1;
}
dfs(SX,SY);
cout<<ans<<endl;
return 0;
}
剪枝
练习
洛谷P1219 [USACO1.5]八皇后 Checker Challenge
题目链接:洛谷P1219 [USACO1.5]八皇后 Checker Challenge
题目描述
一个如下的 6×6 的跳棋棋盘,有六个棋子被放置在棋盘上,使得每行、每列有且只有一个,每条对角线(包括两条主对角线的所有平行线)上至多有一个棋子。
上面的布局可以用序列 2 4 6 1 3 5 来描述,第 i 个数字表示在第 i 行的相应位置有一个棋子,如下:
行号 1 2 3 4 5 6
列号 2 4 6 1 3 5
这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出,解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。
输入格式
一行一个正整数n,表示棋盘是 n×n 大小的。
输出格式
前三行为前三个解,每个解的两个数字之间用一个空格隔开。第四行只有一个数字,表示解的总数。
输入输出样例
输入
6
输出
2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4
说明/提示
【数据范围】
对于 100\%100% 的数据,6 \le n \le 136≤n≤13。
题目翻译来自NOCOW。
USACO Training Section 1.5
解题思路:
相当经典的n皇后问题。
ac题解
//时间:481ms(O2:353ms) 内存:808.00KB
#include<bits/stdc++.h>
using namespace std;
int n;
int row[15],col[15],dia[30],bdia[30];
//row:行,col:列,dia:左上到右下,bdia:左下到右上
long long ans;//总共多少种
void dfs(int step){ //step:当前在第几行
if(step>n){ //n个皇后已经全部放完
if(ans<3) {
for(int i=1;i<=n;i++) cout<<row[i]<<" ";
cout<<endl;
}
ans++;
return;
}
for(int i=1;i<=n;i++){//遍历该行每一个位置
//如果该列,或者两条对角线有其他皇后了,则跳过,查看下一位置
if(col[i]||dia[step-i+n]||bdia[step+i]) continue;
//标记
row[step]=i;
col[i]=1;
dia[step-i+n]=1;
bdia[step+i]=1;
dfs(step+1);//寻找下一皇后的位置
//恢复标记
col[i]=0;
dia[step-i+n]=0;
bdia[step+i]=0;
}
}
int main()
{
cin>>n;
dfs(1);
cout<<ans<<endl;
return 0;
}
洛谷P3956 [NOIP2017 普及组] 棋盘
题目链接:洛谷P3956 [NOIP2017 普及组] 棋盘
题目背景
NOIP2017 普及组 T3
题目描述
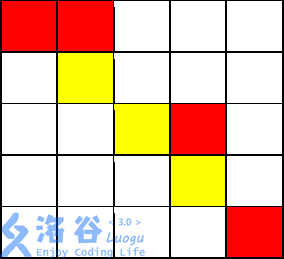
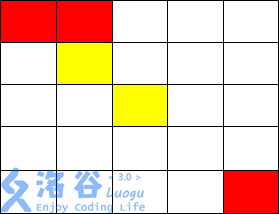
有一个 m×m 的棋盘,棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的), 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 1个金币。
另外, 你可以花费 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用, 而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法; 只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?
输入格式
第一行包含两个正整数m, n,以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的n行,每行三个正整数x, y, c, 分别表示坐标为(x,y)的格子有颜色c。
其中c=1 代表黄色,c=0 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为(1, 1),右下角的坐标为( m, m)。
棋盘上其余的格子都是无色。保证棋盘的左上角,也就是(1, 1)一定是有颜色的。
输出格式
一个整数,表示花费的金币的最小值,如果无法到达,输出-1。
输入输出样例
输入
5 7
1 1 0
1 2 0
2 2 1
3 3 1
3 4 0
4 4 1
5 5 0
输出
8
输入
5 5
1 1 0
1 2 0
2 2 1
3 3 1
5 5 0
输出
-1
说明/提示
输入输出样例 1 说明
从(1,1)开始,走到(1,2)不花费金币
从(1,2)向下走到(2,2)花费 1 枚金币
从(2,2)施展魔法,将(2,3)变为黄色,花费 2 枚金币
从(2,2)走到(2,3)不花费金币
从(2,3)走到(3,3)不花费金币
从(3,3)走到(3,4)花费 1 枚金币
从(3,4)走到(4,4)花费 1 枚金币
从(4,4)施展魔法,将(4,5)变为黄色,花费2 枚金币,
从(4,4)走到(4,5)不花费金币
从(4,5)走到(5,5)花费 11 枚金币
共花费 8枚金币。
输入输出样例 2 说明
从( 1, 1)走到( 1, 2),不花费金币
从( 1, 2)走到( 2, 2),花费1金币
施展魔法将( 2, 3)变为黄色,并从( 2, 2)走到( 2, 3)花费2 金币
从( 2, 3)走到( 3, 3)不花费金币
从( 3, 3)只能施展魔法到达( 3, 2),( 2, 3),( 3, 4),( 4, 3)
而从以上四点均无法到达( 5, 5),故无法到达终点,输出-1
数据规模与约定
对于 30%的数据, 1 ≤ m ≤ 5, 1 ≤ n ≤ 10。
对于 60%的数据, 1 ≤ m ≤ 20, 1 ≤ n ≤ 200。
对于 100%的数据, 1 ≤ m ≤ 100, 1 ≤ n ≤ 1,000。
解题思路:
ac题解
//时间:69ms(O2:63ms) 内存:808.00KB
#include<bits/stdc++.h>
using namespace std;
int m,n;
int ans[105][105],mp[105][105];//ans存取该点最小金币
//mp代表该点颜色,-1无色,0红色,1黄色,2魔法变的红,3魔法变的黄
int ntx[4]={0,0,-1,1};//ntx和nty组成下一步
int nty[4]={1,-1,0,0};
const int INF=999999999;//无穷大
void dfs(int x,int y,int sum){
if(ans[x][y]<=sum){
return;
}else{
ans[x][y]=sum;
}
if(x==m&&y==m) return;
int nx,ny;
for(int i=0;i<4;i++){
nx=x+ntx[i]; //nx,ny为下一步坐标
ny=y+nty[i];
if(nx<1||nx>m||ny<1||ny>m) continue;//如果越界直接跳过
if(mp[x][y]==0){//该点为红色
if(mp[nx][ny]==0){
dfs(nx,ny,sum);
}else if(mp[nx][ny]==1){
dfs(nx,ny,sum+1);
}else if(ans[nx][ny]>sum+2){
mp[nx][ny]=mp[x][y]+2;
dfs(nx,ny,sum+2);
}
}else if(mp[x][y]==1){//该点为黄色
if(mp[nx][ny]==0){
dfs(nx,ny,sum+1);
}else if(mp[nx][ny]==1){
dfs(nx,ny,sum);
}else if(ans[nx][ny]>sum+2){
mp[nx][ny]=mp[x][y]+2;
dfs(nx,ny,sum+2);
}
}else if(mp[x][y]==2){//该点为魔法红色
if(mp[nx][ny]==0){
dfs(nx,ny,sum);
}else if(mp[nx][ny]==1){
dfs(nx,ny,sum+1);
}
}else if(mp[x][y]==3){//该点为魔法黄色
if(mp[nx][ny]==0){
dfs(nx,ny,sum+1);
}else if(mp[nx][ny]==1){
dfs(nx,ny,sum);
}
}
}
}
int main()
{
cin>>m>>n;
int i,j;
for(i=1;i<=m;i++){
for(j=1;j<=m;j++){
ans[i][j]=INF;//初始化每个点最小金币为无穷大
mp[i][j]=-1;//初始化图均为无色
}
}
while(n--){//染色
scanf("%d%d",&i,&j);
scanf("%d",&mp[i][j]);
}
dfs(1,1,0);
if(ans[m][m]==INF) cout<<-1<<endl;
else cout<<ans[m][m]<<endl;
return 0;
}