前言

简介：涉及并查集，题目源于洛谷
建议大家先自行尝试解题，同时阿鑫的水平不高，所以题解也通常并不算好，建议大家可以在洛谷相关题目的题解处查看其他大佬的题解，阿鑫的题解简单看看就好。

并查集是一种树型的数据结构。
可以判断两个元素是否在同一集合内，也可以将各元素合并到各集合内。

并查集基础

首先，如何判断一个元素在哪个集合内呢。
我们可以用一个数组存放其父结点。比如这里用par[]数组来存放其父节点。
par[x]=y 则代表 x 的父节点为 y（x 在 y 的集合内）

所谓并查集，其基础操作便是 初始化、合并、查询。

初始化
首先需要初始化每个元素的父节点为自己，即每个元素就是一个独立集合。

//初始化 
void init(){
    for(int i=1;i<=n;i++){
        par[i]=i;
    }
}

查询
查询该元素位于哪个集合内，如果父节点为自己(par[x]==x)，则代表其为根节点，直接返回。
否则，则接着向上查找。

//查找祖先节点 
int find(int x){
    if(par[x]==x) return x;
    else return find(par[x]);
}

路径压缩
显然对于每个底层节点找根节点是不公平的，效率太低了，父节点有一个就够了。此处画图可能好解释一点。

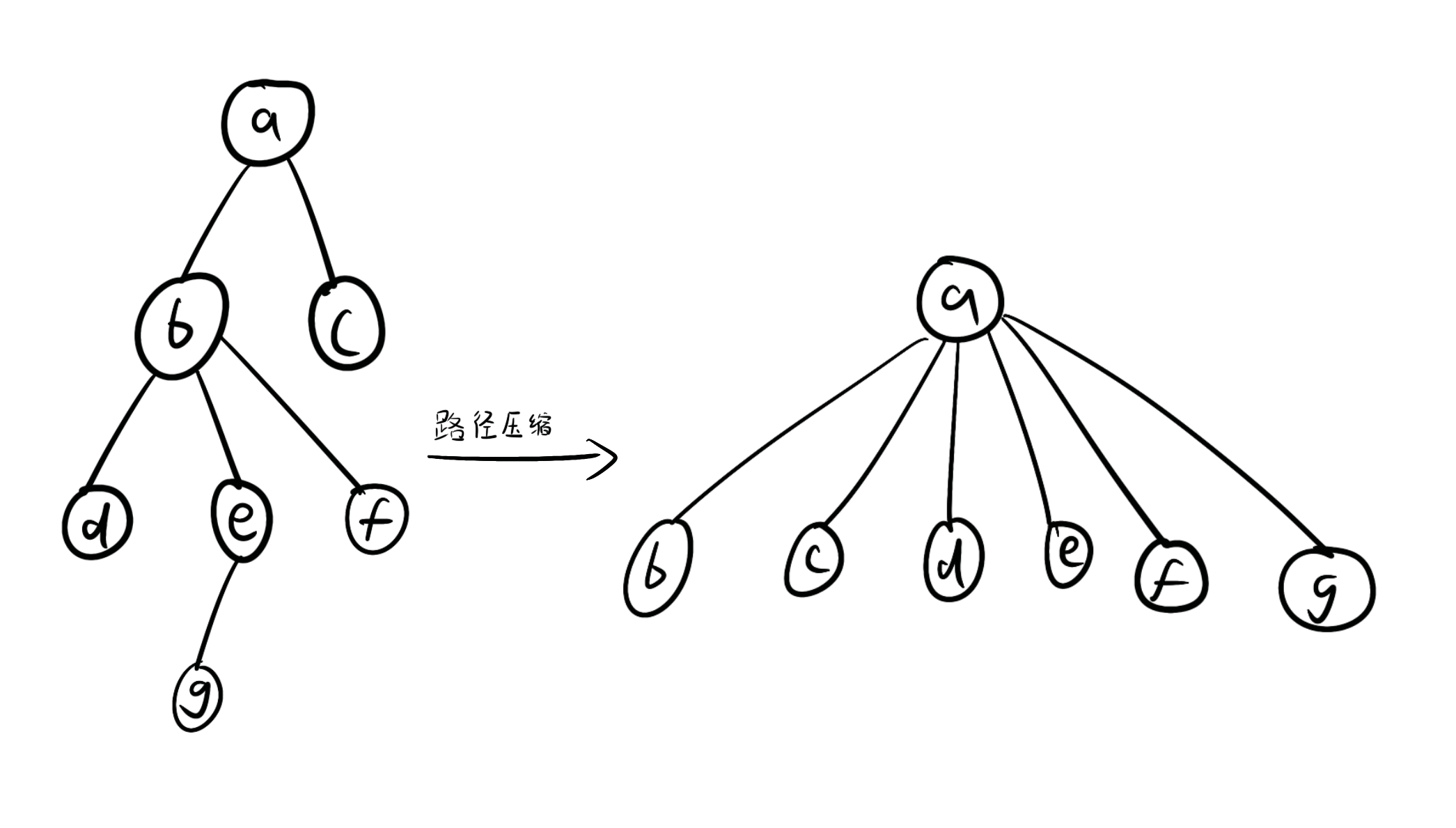
//查找父节点 
int find(int x){
    if(par[x]==x) return x;
    else return par[x]=find(par[x]);
}

合并
对于两个元素，先判断是否在同一集合（即找到并判断其祖先节点是否相等），
如果不在同一集合，（由于暂时不考虑带秩）则将 y 的祖先节点的祖先结点变为 x 的祖先节点。 则向左合并（即将 y 合并到 x 的集合），

//合并 
void merge(int x,int y){
    int tx=find(x);    //找到父节点，下同
    int ty=find(y);
    if(par[tx]!=par[ty])    //如果不在同一集合
        par[ty]=tx; //将 y 的父节点的父结点变为 x 的父节点
}

大概了解后可以尝试做一下简单的模板题

模板题

洛谷P3367 【模板】并查集

题目描述

如题，现在有一个并查集，你需要完成合并和查询操作。

输入格式

第一行包含两个整数 $N,M$ ,表示共有 $N$ 个元素和 $M$ 个操作。
接下来 $M$ 行，每行包含三个整数 $Z_i,X_i,Y_i$ 。
当 $Z_i=1$ 时，将 $X_i$ 与 $Y_i$ 所在的集合合并。
当 $Z_i=2$ 时，输出 $X_i$ 与 $Y_i$ 是否在同一集合内，是的输出 Y ；否则输出 N 。

输出格式

对于每一个 $Z_i=2$ 的操作，都有一行输出，每行包含一个大写字母，为 Y 或者 N 。

样例 #1

样例输入 #1

4 7
2 1 2
1 1 2
2 1 2
1 3 4
2 1 4
1 2 3
2 1 4

样例输出 #1

N
Y
N
Y

提示

对于 $30\%$ 的数据，$N \le 10$，$M \le 20$。
对于 $70\%$ 的数据，$N \le 100$，$M \le 10^3$。
对于 $100\%$ 的数据，$1\le N \le 10^4$，$1\le M \le 2\times 10^5$，$1 \le X_i, Y_i \le N$，$Z_i \in \{ 1, 2 \}$。

ac题解

#include <bits/stdc++.h>

using namespace std;

int n,m,z,x,y;
int par[100005];

//初始化 
void init(){
    for(int i=1;i<=n;i++){
        par[i]=i;
    }
}

//查找父节点 
int find(int x){
    if(par[x]==x) return x;
    else return par[x]=find(par[x]);
}

//合并 
void merge(int x,int y){
    x=find(x);
    y=find(y);
    if(par[x]!=par[y])    par[y]=x;
}

//是否在同一集合 
bool equ(int x,int y){
    if(find(x)==find(y)) return true;
    else return false;
}

int main()
{
    cin>>n>>m;
    int i;

    init();
    for(i=1;i<=m;i++){
        scanf("%d%d%d",&z,&x,&y);
        if(z==1){
            merge(x,y);
        }else if(z==2){
            if(equ(x,y)) cout<<"Y"<<endl;
            else cout<<"N"<<endl;
        }
    }
    return 0;
}

#include <bits/stdc++.h>

using namespace std;

int n,m,z,x,y;
int par[100005],rank[100005];


void init(){
    for(int i=1;i<=n;i++){
        par[i]=i;
    }
}
int find(int x){
    if(par[x]==x) return x;
    else return par[x]=find(par[x]);
}
void merge(int x,int y){
    x=find(x);
    y=find(y);
    if(par[x]!=par[y]){
        if(ran[x]>ran[y]){
            par[y]=x;
        }else{
            if(rank[x]==rank[y])ran[y]++;
            par[x]=y;
        }
    }
}

void equ(int x,int y){
    if(find(x)==find(y))cout<<"Y"<<endl;
    else cout<<"N"<<endl;
}

int main()
{
    cin>>n>>m;
    int i;

    init();
    for(i=1;i<=m;i++){
        scanf("%d%d%d",&z,&x,&y);
        if(z==1){
            merge(x,y);
        }else if(z==2){
            equ(x,y);
        }
    }
    return 0;
}